Limita funkce

Pojem limita se dá dobře intuitivně pochopit. Tato matematická pomůcka nám vyjadřuje, že funkce blíží nějakému konkrétnímu číslu. Právě toto číslo je pak označováno jako limita. Pro práci v diferenciálním a integrálním počtu ji, ale potřebujeme také umět exaktně popsat.

Limitou funkce zkoumáme chování a průběh funkce, když se její nezávislá proměnná blíží nějakému konkrétnímu číslu. Definice limity posloupnosti a funkce se podobají, nicméně hlavním rozdílem mezi nimi je, jakou část můžeme zkoumat. U poslouhostí jsme omezeni jen na index členů posloupnosti, když se blíží nekonečnu.

Zaměřeno na bod

Zjišťujeme chování funkce v okolí bodu $a$. Funkční hodnota limity funkce f v bodě a závisí pouze na chování na okolí bodu a mimo bod a.

V definici se nikde $f(a)$ neobjevuje, nemusí být v bodě definovaná. Předpokládáme, že funkce $f$ je definovaná na tomto okolí bodu $a$ s možnou výjimkou bodu $a$ samotného. Limita funkce má spojitý argument a probíhá podmnožinu ℝ.

Definice limity

Často používaná definice, je zásadní pro rigorózní pochopení limit a prokázání existence limit v různých důkazech.

Definice pomocí okolí bodu

Řekneme, že c ∈ ℝ* je limitou funkce f v bodě a ⇔ $(∀U_c)(∃U_a)(∀x ∈ D_f)(x ∈ U_a-{a} ⇒ f(x) ∈ U_c)$

Známá ε-δ definice

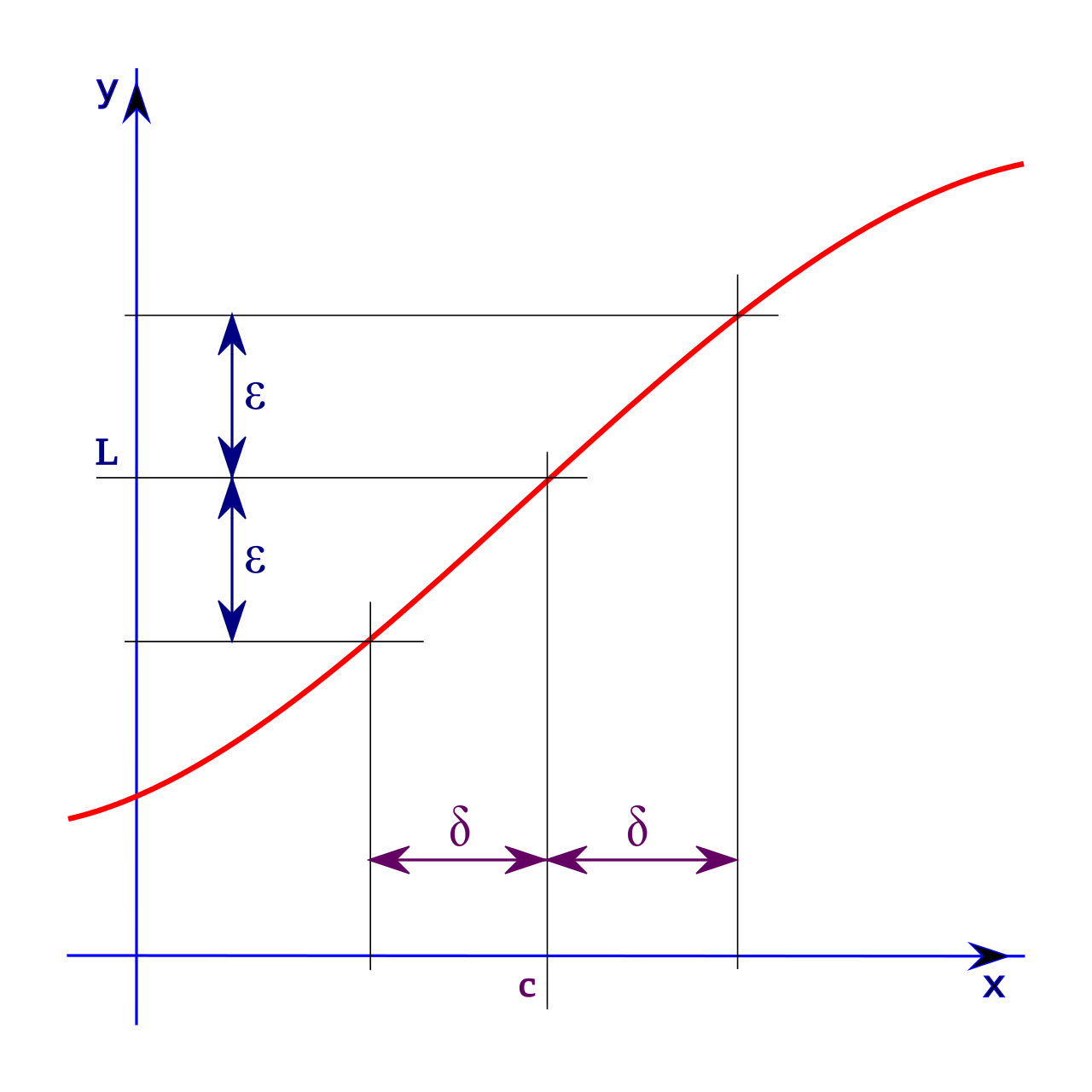
Touto definicí se snažíme říct, že funkce $f(x)$ má v bodě $L$ limitu $c$, jestliže k libovolnému $ε > 0$ existuje takové $δ > 0$, že pro všechna $x$ z δ-okolí bodu $L$, s vyjímkou bodu $L$ je

V této definici, ale ještě rozlišujeme tzv. vlastní a nevlastní body. Vlastním bodem je myšleno, když $L$ i $c$ jsou prvky ℝ reálné číslo, nevlastním pak ∞ či -∞. Stejně tak říkáme, že limita je vlastní, pokud se jedná o reálné číslo a nevlastní, pokud je hodnota limity ∞ či -∞.

Pro vlastní limitu $\lim\limits_{x \to L} f(x) = c$ je pak celá definice

$(∀ε > 0)(∃δ > 0)(∀x ∈ D_f)(0 < |x−L| < δ ⇒ |f(x) − c| < ε)$

Limita součtu, podíl a součinu

Mějme $f: A\to ℝ$ a $g: B\toℝ$ funkce a bod $a ∈ A$. Potom platí: $\lim\limits_{x \to a} (f(x) ± g(x)) = \lim\limits_{x \to a}f(x) ± \lim\limits_{x \to a}g(x)$

$\lim\limits_{x \to a} f(x)·g(x) = \lim\limits_{x \to a}f(x)·\lim\limits_{x \to a}g(x)$

$\lim\limits_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim\limits_{a}f(x)}{\lim\limits_{a}g(x)}$

Věta o limitě složené funkce

Nechť f a g jsou funkce, a, b, c jsou prvky ℝ* a platí tři postačující podmínky

$\lim\limits_{x \to b} f(x) = c$

$\lim\limits_{x \to a} g(x) = b$

$(∃Ha)(∀x ∈ D_g ∩ H_a-{a})(g(x) != b) nebo (b ∈ D_f a f(b) = c)$

Potom $\lim\limits_{x \to a} f(g(x)) = c$

Poznámka k 3. bodu: funkční hodnota vnitřní funkce musí být v $D_f$ a vnější musí být spojitá v bodě $c$.

Příklad, plynoucí z věty o limitě složené funkci

Buď $P(x)$ libovolný polynom a $a ∈ ℝ$. Potom $\lim\limits_{x \to a} P(x) = P(a)$. Tzn. Pouze dosadíme za x vlastní limitu.

$\lim\limits_{x \to 1} e^{-\frac{-1}{(x-1)^2}}$.

1. Označíme $f(x) = e^x$ a $g(x) = -\frac{-1}{(x-1)^2}$
2. $\lim\limits_{x \to 1} = -\frac{-1}{(x-1)^2} = - \infty$
3. $\lim\limits_{x \to -\infty} = e^x = 0$

Dále např. pro $H_1(1)$ = platí $g(x) != -∞$ pro všechna x ∈ H_1\{1}. Tedy první možnost v 3. předpokladu je splněna. Díky větě o limitě složené funkci dostáváme výsledek.

Nerovnosti a limity

Nechť existují limity $\lim\limits_{x \to a} f(x)$ a $\lim\limits_{x \to a} g(x)$. Pak platí dvě tvrzení:

1. Pokud $\lim\limits_{x \to a} f(x) < \lim\limits_{x \to a} g(x)$, potom $∃H_a$ a takové, že pro všechna $x ∈ H_a-{a}$ platí $f(x) < g(x)$.

2. Pokud existuje okolí $H_a$ bodu a takové, že pro všechna $x∈H_a∖{a}$ je $f(x)≤g(x)$, potom $\lim\limits_{x \to a} f(x) ≤ \lim\limits_{x \to a} g(x)$

Věta o limitě sevřené funkce

Nechť pro funkce $f, g, h$ a body $a, c ∈ ℝ*$ platí:

• existuje okolí Ha bodu a takové, že pro každé $x ∈ Ha/{a}$ platí $f(x) ≤ g(x) ≤ h(x)$,
• existují $limx→a f(x) = limx→a h(x) = c$. Potom existuje i limita $limx→a g(x)$ a je rovna c.