Primitivní funkce
Nechť funkce f je definována na intervalu (a,b), kde -∞ ≤ a, < b ≤ ∞. Funkci F splňující podmínku $F'(x) = f(x)$ pro každé $x ∈ (a, b)$
Poznámka: F je diferencovaltená v každém bodě na intervalu.
Věta (Postačující podmínka pro existenci primitivní funkce): Nechť funkce f je spojitá na intervalu (a, b). Pak funkce f má na tomto intervalu primitivní funkci.
Neurčitý integrál
Nechť k funkci f existuje primitivní funkce na intervalu (a, b). Množinu všech primitivních funkcí k funkci f na (a,b) nazýváme neurčitým integrálem a značíme jej $\displaystyle \int f$ nebo $\displaystyle \int f(x) d x $.
Per partes (Integrace součinu)
VĚTA: Nechť funkce f je diferencovatelná v intervalu (a, b) a G je primitivní funkce k funkci g na intervalu (a, b) a konečně nechť existuje primitivní funkce k funkci f'G. Potom existuje primitivní funkce k funkci fg a platí
$\int fg = fG - \int f'G$
DÚKAZ:
Tvrzení věty můžeme přímo ověřit derivováním
$(fG - \int f'G)' = (fG)' − f'G = f'G + fG' − f'G = fG' = fg$
Zapamatování formule. 1. výraz zderivuj, 2. zintegruj. Součin na diagonále, mínus poslední řádek.
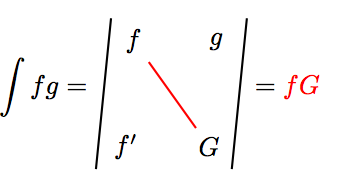
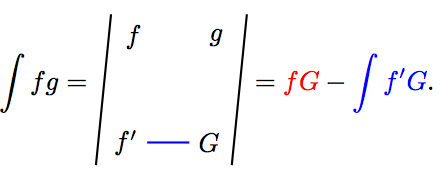
Substituce
VĚTA: Nechť f je diferencovatelná na (a, b) a ϕ na (α, β) a nechť:
- f má primitivní funkci F na intervalu (a, b)
- ϕ je na intervalu (α, β) diferencovatelná,
- ϕ(α, β) ⊂ (a, b).
Pak funkce f(ϕ(x))·ϕ'(x) má primitivní funkci na intervalu (α, β) a platí
$\int f(ϕ(x))·ϕ'(x) dx = F(ϕ(x)) + C. $